If changes in both T and % RH are simultaneously made to a paper’s environment the resulting deterioration rate will reflect their combined effects. This combined effect on the rate ratio is the product of the individual ratio effects. Therefore, by multiplying Equations 2 and 3 we get the overall effect on deterioration rates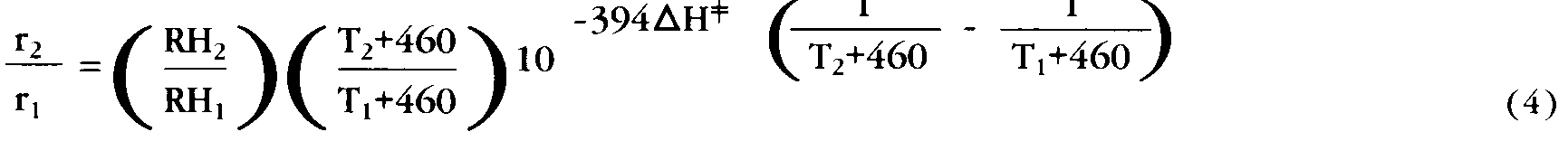
Equation 4
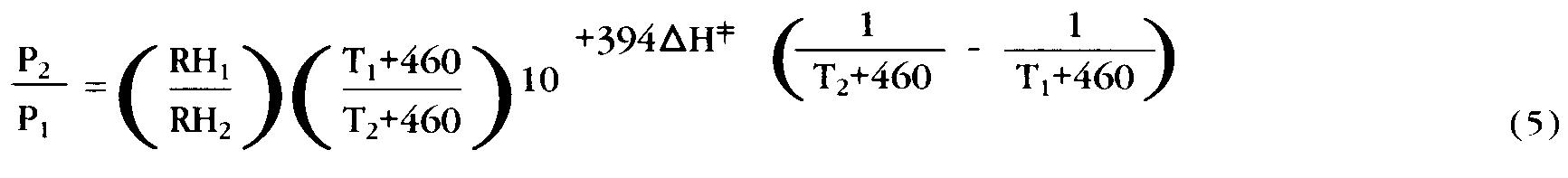
Equation 5
Using the appropriate environmental values for the T’s and RH’s and an estimated or experimentally determined value for ![]() these equations can be evaluated algebraically to obtain a quantitative evaluation of permanence changes.
these equations can be evaluated algebraically to obtain a quantitative evaluation of permanence changes.
Definition of Isoperm
Algebraic computations using Equation 5 would be time consuming if not daunting to all except those with mathematical interests and skills. The equation would be more readily usable if cast in graphical form. The next paragraph, which describes this transformation, is the key to the isoperm method.
Consider a paper at equilibrium with some initial conditions of temperature and relative humidity that determine its rate of deterioration and permanence. Now let us increase the relative humidity to a higher value; if the temperature is unchanged, the rate of deterioration will increase. However, if we reduce the temperature by exactly the right amount, the resulting temperature induced rate decrease will exactly compensate for the relative humidity induced increase so the overall deterioration rate (and permanence) is unchanged from that at the initial environmental conditions. We can make another change in relative humidity (or temperature), and another temperature (or relative humidity) can be found that again will exactly compensate for the new relative humidity (or temperature) induced permanence change. There is, of course, an infinite set of such paired T and % RH conditions, all associated with the same permanence value. These paired values when plotted on a graph of T and % RH as axes generate a line. This line of constant permanence (isopermanence) is defined as an isoperm. Figure 1 is such a graph.
Erratum:In the following formulae, the printed text contains an error. The highest value on the Y-Axis of Figures 1, 2, 3, 4 and 5, should read 110° F
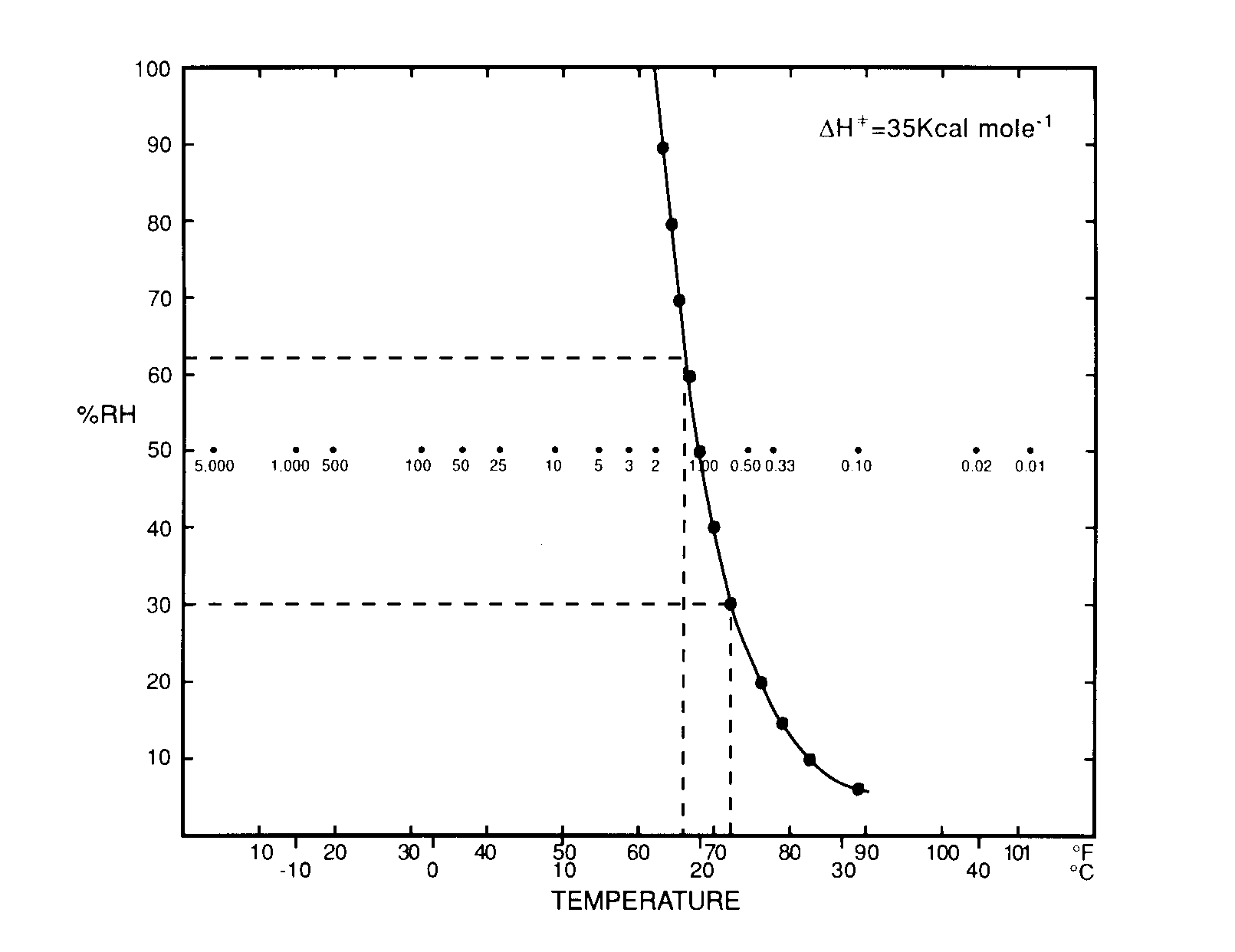
Fig. 1. Construction of an Isoperm. Paper permanence value at 68 degrees and 50% RH is assigned a relative value of 1.00. Other temperature and relative humidity conditions which also have permanence value of 1.00 are plotted and joined to yield an Isoperm of value 1.00. Valules of permanence at 50% RH and various temperatures are shown.
A 68 degrees F temperature and 50% RH is arbitrarily selected as the initial or reference environmental state of permanence, P1. Any other T and % RH values could have been selected as a reference state but 68 degrees F/50% RH is reasonably close to common storage conditions and so can serve as a useful basis or standard for comparison with other conditions. The other paired points, and thus the overall shape of the isoperm, is established by computation from Equation 5. In the calculation, a value of 35 Kcal is used for deltah=| and the relative humidity is changed by 10% increments; the temperature which keeps the permanence equal to that at 68 degrees F/50% RH is calculated and the paired points are connected. The resulting isoperm line is labelled 1.0 since it shows conditions where all P2’s equal P1, as the relative permanence is unchanged P2/p1=1.0.
What does the isoperm value of 1.0 on the graph mean? For now, as a first illustration we can say that if a paper had a 45 (or 90 or 300) year life expectancy at 68 degrees F/50% RH it will have the same permanence (45, 90 or 300 years) at any environmental conditions along that line–at 72 degrees F/30% RH or 66 degrees F/62% RH for example.
Figure 1 also displays the temperature (at 50% RH) corresponding to permanence values greater and less than 68 degrees F/50% RH. The isoperm values of 5.0 and 0.33 at 54 degrees F and 78 degrees F respectively mean that the paper of 45 years permanence at 68 degrees F would require 225 years to attain the same state of deterioration at 54 degrees F, but only 15 years to attain the same state of deterioration at 78 degrees F.
Figures 2 and 3 display a completed array of isoperms for ![]() values of 25 and 35 Kcal drawn for selected relative permanence values.Other isoperms can be calculated from Equation 5 or are easily estimated by interpolation. It is evident that while the two diagrams are very similar, the 35 Kcal graph shows a greater “sensitivity” to temperature changes. Taken together they both show the importance of using the appropriate
values of 25 and 35 Kcal drawn for selected relative permanence values.Other isoperms can be calculated from Equation 5 or are easily estimated by interpolation. It is evident that while the two diagrams are very similar, the 35 Kcal graph shows a greater “sensitivity” to temperature changes. Taken together they both show the importance of using the appropriate ![]() for a collection.
for a collection.
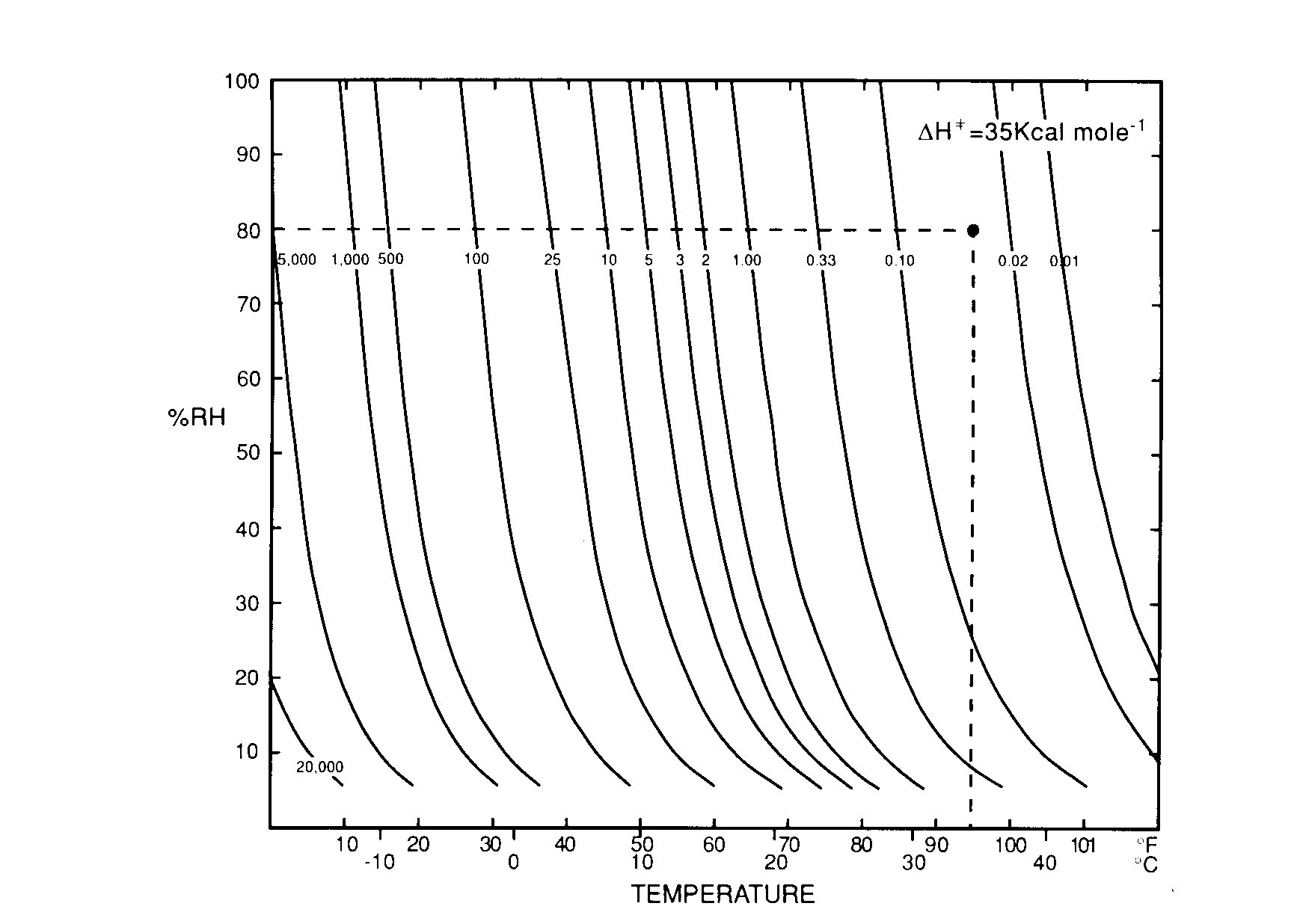
Fig. 2. Percent relative humidity versus temperature Isoperm diagram. Permanence
values are calculated for ![]() = 35 kcal relative to paper at 68 degrees F and 50% RH taken as comparison standard (permanence equal to 1.00). Relative permanence at 95 degrees F and 80% RH is 0.03.
= 35 kcal relative to paper at 68 degrees F and 50% RH taken as comparison standard (permanence equal to 1.00). Relative permanence at 95 degrees F and 80% RH is 0.03.
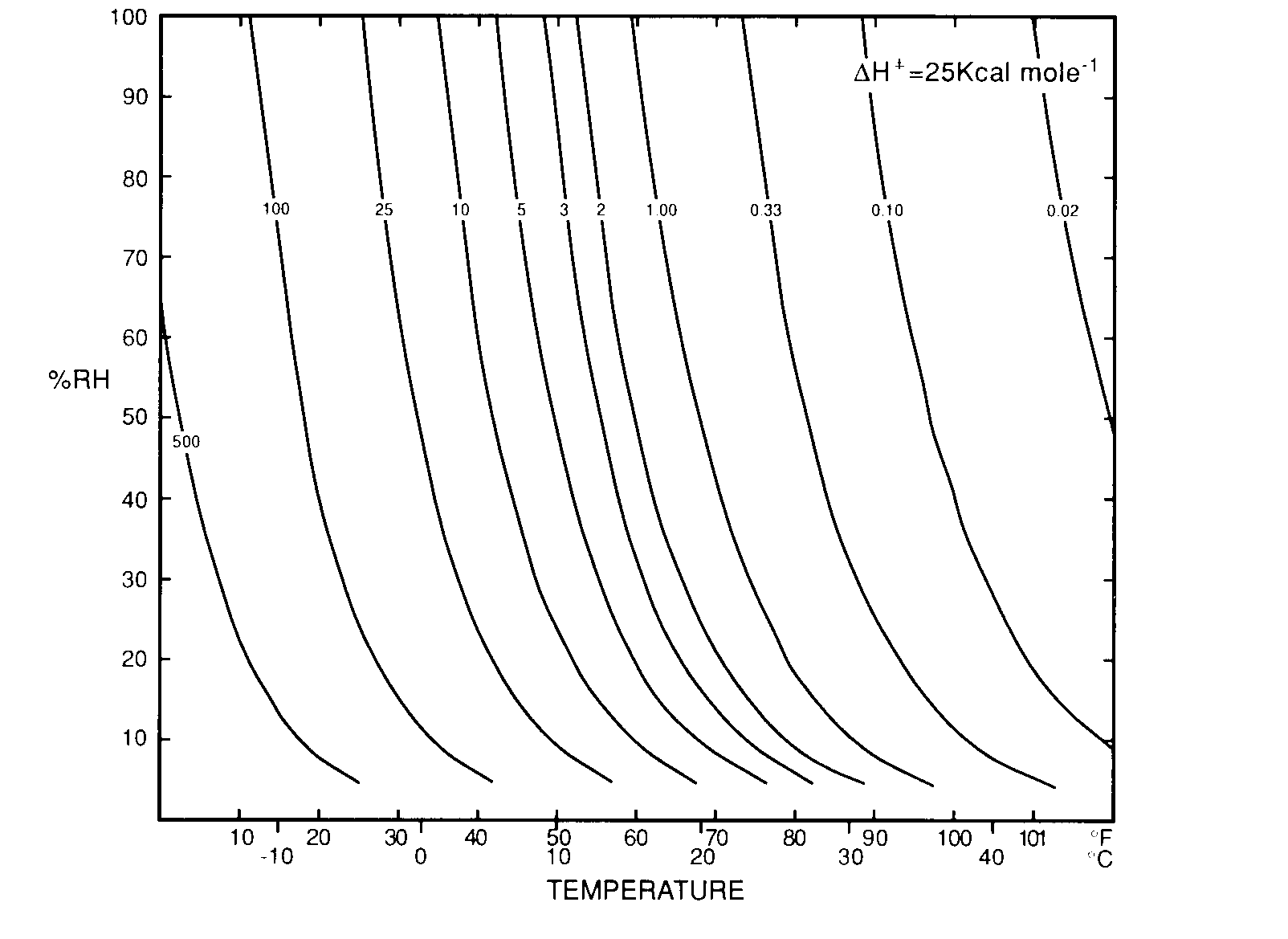
Fig. 3. Percent relative humidity versus temperature isoperm diagram. Permanence values are calculated for![]() = 25 kcal mole -1 relative to paper at 68 degrees F/50% RH taken are reference standard (isoperm equals 1.00).
= 25 kcal mole -1 relative to paper at 68 degrees F/50% RH taken are reference standard (isoperm equals 1.00).
It should be noted that for the narrow range of T and % RH commonly encountered in research libraries and archives, the uncertainty introduced is relatively small and probably insignificant for most practical purposes.

