It is appropriate at this point, now that the isoperm concept and some of its applications are understood, to examine in greater detail the factors which affect the numerical values of isoperms. The values generated thus far arise from choices of parameters and assumptions which, though useful for expository and illustrative purposes, may not be best for a specific collection. The following discussion illustrates how the isoperm assumptions (and so Equations 4 and 5 and the resultant % RH vs T isoperm diagrams) can be modified to incorporate new experiential information.
In the development of Equation 4 the dependence of deterioration rate on % RH was taken as linear and so the relative deterioration rate at two different % RH’s is also linear. This is expressed mathematically in Equation 2 as raising the ratio of % RH’s to the first power.
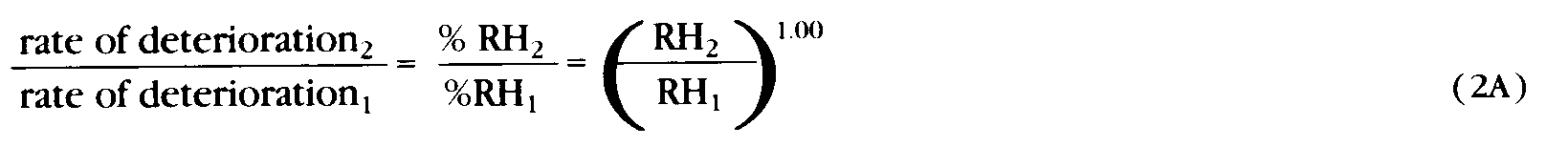
Some studies suggest that the deterioration rate is more sensitive to relative humidity than a linear dependence. For some papers in the middle ranges of % RH ( 30-60%) the dependence may be the power 1.4 rather than 1.0, thus the relative humidity component of Equation 5 would be the following.
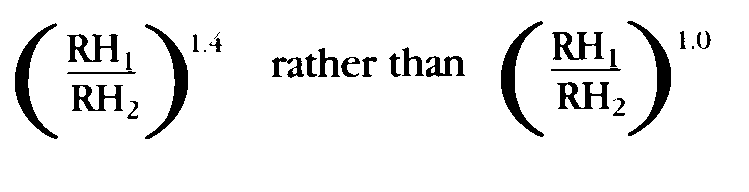
The consequence of this change to the % RH vs T isoperm diagram would be to somewhat decrease the steepness of the slope of each isoperm line. We can estimate the magnitude of this effect at the %RH limits likely to be encountered in a collection controlled by and HVAC system (30-60% RH). The relative humidity contribution to the isoperm value would become
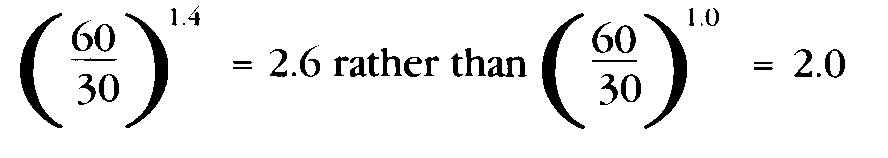
A change in value of this magnitude, i.e., 30%, while itself significant, may not affect a management decision based upon life expectancy differences of 200-300% or more.
More significant is the selection of an appropriate value of 
.As can be seen by comparing Figures 2 and 3, the difference between ‘s of 25 and 35 Kcal is substantial, especially for large temperature changes. The 35 Kcal value used in the examples was selected in part because it resulted in larger, more easily recognized differences while still being a value appropriate to many papers. The precise choice of a particular value will unquestionably depend in considerable part upon the specific papers in the collection as well as the manner in which they are housed (bound books, boxed manuscripts, newspapers, and so forth). For some of these collections at least, a value of 25 Kcal may be more appropriate and the % RH vs T isoperm diagram of Figure 2 may be more appropriate than Figure 3.The numerical values of isoperms discussed in the illustrations of stated paper should not be taken as necessarily the best for all situations. The preservation manager, before making decisions and committing expenditure of funds, should seek the advice of experts or carefully review the most recent literature. Indeed, the need for more specific temperature dependency data has been recognized by the preservation community and proposals have been made to conduct such studies to obtain more information.
While awaiting these studies and expert advice, the preservation manager can explore the preservation consequences using both the 25 and 35 Kcal isoperm diagrams. Such a comparison will show the differences in isoperm value associated with this range of values and suggest whether the differences are large enough to significantly affect the manager’s decision.
Another even more cautious and conservative approach would be to utilize the 35 Kcal % RH vs T diagram for isoperm values below 1.0 and the 25 Kcal diagram for isoperm values above 1.0. This would have the effect of increasing (exaggerating?) the anticipated harmful effects of higher temperatures, and decreasing (under estimating?) the life expectancy consequences of lowering temperatures. Though such approximations may be sufficient to provide the basis for a management decision, they cannot, of course, provide the confidence inspired by developing and using the isoperm values most appropriate to a given collection
