A Different Approach to the Evaluation of Research Libraries
In 1996, within a program funded by The Andrew W. Mellon Foundation to encourage research on the economics of information, the Council on Library and Information Resources made a grant to Rutgers University for a project in the School of Communication, Information, and Library Studies that would apply new economic theories to measuring how well research libraries fulfill their service roles. The following summary draws on the original proposal and the final report from the project’s directors, Wonsik Shim and Paul B. Kantor. Regrettably, it cannot reproduce the full array of figures and charts through which they present the details of their argument.
The evaluation of library performance is problematic, in part because the principal products of a library are services that lead to an intangible result, the acquisition of knowledge. It’s possible to study the service activities of libraries as service activities and assess how well they are performed, but even this narrow focus encounters a major difficulty. Libraries deliver a complex mix of services and consume a complex mix of resources. Some resources may be more expensive for some libraries than for others, and some services may be more important than others. The mix varies from library to library, giving precise meaning to the observation that each library is different from every other library.
In the absence of better measures, university librarians have historically resorted to calculating performance through ratios derived from data the libraries supply annually to the Association of Research Libraries (ARL). Examples of these ratios include : professional staff as a percentage of total staff, library materials expenditures as a percentage of total library expenditures, the number of items loaned as against the number of items borrowed, and serials expenditures per faculty member.
These measures are limited in two ways, explain Shim and Kantor. First, almost all the ratios look only to the input side of library operations. There is no attempt to contrast the inputs with the outputs, such as reference transactions, the circulation of materials, and interlibrary loans. Second, because so many ratios are derived from the ARL data (about 30 in all), each library can pick and choose only those according to which it performed well (or at least better than other institutions). Although these rankings are easy to compute and understand, they do not provide a solid basis for judging peers, or a foundation upon which to build improvement.
Shim and Kantor offer the following comments on the shortcomings of the traditional models for measurement: “They do not recognize that it is far more important to identify excellence than to identify mediocrity. Knowledge of the mean or average behavior is of little help to any manager, since even those who fall, in some sense, below the mean, are not simply striving to become average. Each library unit would like to be not just above average but outstanding.”
The Rutgers research team argues that a different theoretical approach, drawn from economics and operations research, will provide a better understanding of the efficiency of academic research libraries. Their analytical tool (which they believe has the potential to be applied as well in the digital library environment) is called Data Envelopment Analysis (DEA). This new approach represents the convergence of two streams of theoretical research-the economic study of production functions and the application of an optimization technique called linear programming to define “best practices” among the group of entities chosen for examination. DEA considers a collection of comparable entities, usually called “decision-making units” (DMUs). Some are identified as “frontier units.” Others are compared with the frontier units, and their performance is scored as a percentage of the performance that would be needed to place them on the frontier.
Thus, DEA, applied to a proper model of inputs and outputs for libraries, will show the best practices in peer groups of institutions and allow calculation of a technical efficiency score for each library. Instead of revealing the average performance among a group of libraries, the process will characterize each library in terms of its efficiency relative to a specific peer group of libraries, which may be more efficient than the library at hand when all are evaluated using the same weights and proportionality factors.
Data Envelopment Analysis (DEA)
DEA was developed to measure the relative efficiencies of “decision-making units” with multiple inputs and outputs. A “DMU” can be any component within a managed organization-from an entire firm, to a plant, to a single operation within the plant. The DEA technique has been applied to DMUs as diverse as banks, police departments, hospitals, tax offices, prisons, defense bases, schools, and university departments. In the Rutgers project, the unit of analysis is an entire library.
Shim and Kantor employ DEA to determine, in brief, the relative efficiency of a set of libraries when each library is allowed to be best represented in its mix of inputs and outputs. They use the following ten inputs and five outputs for a given year:
Inputs
-
- : total volumes held, net volumes added, monographs purchased, total current serials, number of professional staff, number of support staff, number of student employees (FTE), number of full-time students, total graduate student enrollment, and number of full-time faculty members.
Outputs
- : total interlibrary lending, total interlibrary borrowing, the number of students who participated in instructional classes in the library, reference transactions, total circulation.
The efficiency is calculated by forming the ratio of a weighted sum of outputs to a weighted sum of inputs, where the weights (multipliers) for both outputs and inputs are selected in a manner that most favors the focus library. Weights reflect the different levels of cost of inputs and the relative worth (or cost) of outputs. To illustrate, consider two libraries that have two similar pairs of inputs and outputs.
| Books | Librarians | Circulation | Reference | |
| Library A | 1,000 | 10 | 2,000 | 500 |
| Library B | 500 | 8 | 2,500 | 600 |
Assume that a staff person costs about 500 times as much as a book, and that a reference transaction costs ten times as much as a circulation transaction. The corresponding costs are then as follows:
| Books | Librarians | Circulation | Reference | |
| Library A | 1,000 | 5,000 | 2,000 | 5,000 |
| Library B | 500 | 4,000 | 2,500 | 6,000 |
In this situation, Library B is always more efficient because it generates more output with less input. No matter how Library A manipulates the weights for its advantage, it cannot surpass Library B because A must allow B to use the same weights that make A look as good as possible.
Deciding how to assign the weights is by no means an easy task. Though DEA permits each library to “rearrange the world” so that it looks as efficient as possible, there are limitations and constraints on the distortions that are permitted. For example, if a staff person costs $40,000 a year, and a book costs $50, it would be unreasonable to let the DEA program set those two weights as equal. Shim and Kantor examine data available in the published literature and allow large, but not insupportable, variation around the median values therein reported. For example, the numbers given would lead to a ratio of 40,000/50 = 800. Under what Shim and Kantor call a “two-fold range,” they permit a variation from 400 (half the observed value) to 1,600 (twice the observed value). Under what they call a “four-fold range,” this ratio would be allowed to vary from a low of 200 to a high of 3200. This range may seem too generous, yet there is evidence, both anecdotal and quantitative, to suggest that the efficiency of library organizations does vary by as much as a factor of four from the mean or the average when it is measured by a simple ratio. With respect to outputs, it can be said that the contexts of libraries differ enormously, and it is quite conceivable that the relative value of, say, reference and circulation might vary by a factor of 4 or 16 from one setting to another.
The inefficiency of libraries in the study is represented in terms of the proportional reduction of inputs required for an inefficient library to become efficient. In revealing the inefficient libraries, the DEA technique reveals as well a set of best performers.
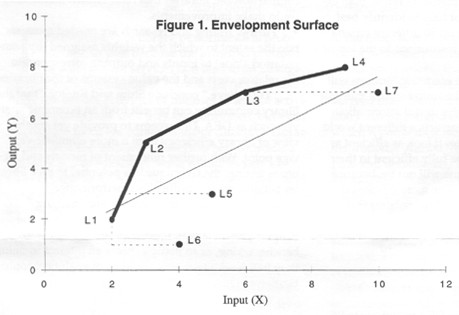
The figure shows 7 DMUs that have only one input and one output. DMUs are assigned the coordinate values associated with the points L1 through L7. A single regression equation used to describe these 7 DMUs (the thin line shown in the figure) represents the average relation between the input (independent variable) and the output (dependent variable). What DEA does is to optimize each DMU against all by giving different weights for each input and output until the most favorable combination is found. Because DEA operates with real data, it will identify a set of DMUs in the population whose efficiency score equals 1. In the figure, this set corresponds to DMUs 1 through 4 (L1-L4). These points describe several versions of the best that one DMU can achieve in a realistic situation. The heavy line connecting these efficient DMUs is called the “envelopment surface” because it envelops all the cases (thus the name “Data Envelopment Analysis”). The dotted lines from the inefficient DMUs (L5-L7) depict graphically the reduction in inputs necessary for these libraries to become efficient. Note that L7 is compared with L3, and L5 is compared with a mix of L1 and L2. L6, being compared with L1, can reduce its inputs and yet still remain deficient in outputs.
Shim and Kantor set down two essential guidelines for the use of DEA in their project:
- There must be a comparison set of libraries as the basis for all the calculations. In this sense, DEA is an extension of the notion of benchmarking. In benchmarking, one does not provide an absolute measure of performance but measures each institution by comparing it with the best performance in a designated peer group. If there are five institutions, and some single measure of performance whose value is 25, 50, 60, 100, and 150 at the five institutions, then the corresponding efficiency scores would be 17%, 33%, 40%, 67%, and 100%. If the top-ranked library were to be removed from the peer group, the scores of the remaining libraries-25, 50, 60, and 100-would yield efficiencies of 25%, 50%, 60%, and 100%.
- Each library is given the benefit of the doubt in determining the relative importance of the various inputs and outputs. For example, if a library consumes a high amount of staff resources, it will be favored in the analysis if the effective cost of staff is set to a low value. If another library has a very large collection, it will be favored in the analysis if the effective cost of a volume is set low, and so forth. In DEA, a separate calculation is done for each library. In this calculation, the effective costs and the values of services are adjusted to make the focus library look as good as possible. If it looks at least as good as any other library from this perspective, it receives an efficiency score of 1. But if some other library looks better than the focus library, even when the world is described in a way that is most favorable to the focus library, it receives an efficiency score of less than 1.
DEA has several advantages over traditional evaluation methods such as rankings or ratios. First, it provides, for each library, a single summary score-the relative efficiency. Depending on the specific DEA model one has applied, this efficiency score reveals, for example, how much (proportional) reduction of inputs or (proportional) augmentation of outputs should be possible if the practices of the most efficient DMUs are adopted. Second, DEA identifies possible improvements with reference to an observable peer group with similar operations. The improvements are derived from reality, not from some ideal goal set by arbitrary means.
Benchmarking and DEA
The use of benchmarking is not uncommon in higher education these days. Simply put, say Shim and Kantor, benchmarking is about learning from the industry leaders. In industry, the most common purposes of benchmarking are to increase customer satisfaction and to reduce costs. Traditional approaches to library evaluation are not particularly useful for benchmarking because they fail to indicate which institutions are the leaders in the academic library community. Library statistics based on the “central tendency” (most notably, the calculation of mean and median) characterize libraries whose performance is mediocre rather than exceptional. Such statistics do not help to identify best practices. And rankings based on 30 different criteria almost never send one or two institutions to the top of all lists.
To adapt benchmarking to academic libraries will require a methodology that takes into account multiple inputs and outputs and provides useful information for peer comparison. DEA constructs a different world view for each library and makes it look as efficient as possible. Many libraries will be fully efficient in their own best world views, but some will not be, because they are essentially inefficient. The more efficient libraries have mixes of policies and procedures that make them more efficient, and those policies and procedures can be adopted by others, with a corresponding improvement in efficiency.
The Results of the Project
The Rutgers project applied the DEA technique to 95 U.S. academic research libraries, using the annual statistics for 1995 and 1996 furnished by members to the Association of Research Libraries. The researchers protected the anonymity of the individual libraries because none expected their data to be subject to this kind of analysis. The libraries were grouped as public (65) and private (30) for comparison.
As noted above, the researchers selected ten variables for inputs, representing collection, staff, and university characteristics, and five service measures for outputs. After setting various reasonable constraints on the weights DEA assigns to inputs and outputs, they used specialized DEA software to calculate the efficiency scores of libraries. They summarize the results as follows:
- Even with the strictest constraints, at least one third of all libraries turned out to be efficient.
- Adding more constraints revealed inefficiency at more libraries.
- Compared with the public group, the private group had a smaller proportion of inefficient libraries, suggesting that, as the size of the comparison group decreases, the chance that the focus library will appear efficient increases.
- The efficiency scores over the two-year period showed a high level of consistency, which argues for the reliability of the technique.
- For each library evaluated as inefficient, DEA produced a set of efficient libraries that were referenced in the process of identifying the library’s inefficiency. By adopting the policies and procedures of libraries in the comparison set, libraries that have shown inefficiency could make improvements.
- Further testing and research are needed to ascertain the extent to which the weights assigned (by computation alone) to inputs and outputs correspond to the relative costs and the value systems of the libraries.
“We believe,” conclude Shim and Kantor, “that the library community can benefit from an economic analysis such as DEA. DEA seems to provide yet another view of library efficiency from a more wholistic vantage point. With further refinement of models and rigorous testing, the technique has potential to give libraries better tools for justification, performance comparison among peers, and decision making.”
Perhaps the largest point to be drawn from the Rutgers project is that, if libraries are to engage in benchmarking, as so many express an interest in doing, they will need a tool with the level of analytical sophistication of DEA.
For information about Data Envelopment Analysis, Shim and Kantor cite the following:
Charnes, A., Cooper, W.W., Lewin, A.Y., and Seiford, L.M. Data Envelopment Analysis: Theory, Methodology, and Application. Kluwer Academic Publishers. Boston. 1994. 513pp.
Easun, M.S. Identifying Efficiencies in Resource Management: An Application of Data Envelopment Analysis to Selected School Libraries in California. Dissertation. University of California, Berkeley. 1992. 521pp.
Research Briefs are occasional papers published by the Council on Library and Information Resources (CLIR) to describe the outcome, or the current status, of projects undertaken within its programs. CLIR encourages duplication of these papers and requires no permission for their further distribution.

